Quote:
Originally Posted by Dragoneye
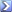
2+2=4...
If the numbers are just measures of units and have no properties, then they must have an associated unit. If they don't, then they cannot be a measure of anything; which means the definition of the numbers is false; which means that which you wrote does not exist. So those numbers must have a a 'default', universal unit that allows them to exist or else your proof that 2+2<>4is invalid because it is grounded in a false truth that the numbers are indeed a measure of something.
The only constant unit(by your definition) is distance. Inches, feet, yards, milimeters, or nanometers; the numbers are implied to be a measure of distance unless another unit is otherwise specified.
Therefore 2 + 2 = 4.
Wow...I needed this. Talk about a brain excercise...
|
Best response I've seen yet, but not completely correct. Since the unit is implied, it is still connected to the number. As I have stated before, to correctly write the formula, you must include units after the 2's. The shorthand is commonly known at 2 + 2 = 4, but the written statement is false.
Also, BTW. Something I just realized and wanted to ask. Why would anyone want to add 2 + 2 in the first place if there's no specified units?